1.4. 确定概率的方法

在概率的公理化体系建立之前，概率可以用其他的定义方法：频率定义、古典定义、几何定义和主观定义。

Remark 1.2

主观定义可以自行阅读《概率论与数理统计教程》P26。

我们将所感兴趣的事件记为 \(A\) ，以下介绍三种计算事件 \(A\) 的概率 \(P(A)\) 的方法。

1.4.1. 频率方法

在频率方法中，假定与事件 \(A\) 有关的随机现象可大量重复进行。在 \(n\) 次重复试验中，记 \(n(A)\) 为事件 \(A\) 出现的次数（也称频数），利用频率 \(f_n(A) = \frac{n(A)}{n}\) 来确定事件 \(A\) 的概率。

人们长期实践表明：随着试验次数 \(n\) 增加，频率 \(f_n(A)\) 会稳定在某一常数附近，称这个常数为频率的稳定值。这个稳定值就是我们所想要求的概率。

频率方法的优点是简单计算，当试验重复次数 \(n\) 较大时，频率方法是合理的。同时，频率方法所得到的概率是满足概率的公理化定义的。但是它的缺点在于，在现实世界里，人们无法把一个试验无限次地重复下去。所以，频率方法只能得到“真实”概率的近似值。

Remark 1.3

频率方法来确定概率是有理论保证的，感兴趣的同学可以阅读大数定律。

在实际生活中，频率是十分常用的，而且十分好用。

Example 1.4 (英文字母的频率)

在很早之前，人们有一种共识：英文字母的出现频率是不同的。某些字母的出现频率高于其他的字母，见表 Table 1.5。

Table 1.5 英文字母的使用频率

字母	使用频率	字母	使用频率	字母	使用频率
E	0.1268	L	0.0394	P	0.0186
T	0.0978	D	0.0389	B	0.0156
A	0.0788	U	0.0280	V	0.0102
O	0.0.0776	C	0.0268	K	0.0060
I	0.0707	F	0.0256	X	0.0016
N	0.0706	M	0.0244	J	0.0010
S	0.0638	W	0.0214	Q	0.0009
R	0.0594	Y	0.0202	Z	0.0006
H	0.0573	G	0.0187

在侦探小说《福尔摩斯探案集》中《跳舞的小人》一篇故事中，福尔摩斯利用英文字母的频率表来破解芝加哥犯罪份子的密码，见图 Fig. 1.1。

Fig. 1.1 跳舞小人密码

感兴趣的同学可以利用课余时间看看能否破解跳舞小人背后的密码？

Hint

你看看你需要几条线索才能破译跳舞小人的密码？

• 每一个小人表示一个英文字母。

• 旗帜表示一个单词的结束。

• 因为是非正式书写，部分字母需要补充意思才能完整。

• 接受信息对象的名字是埃尔西（Elsie）。

• 接受信息对象居住地点在埃尔里奇（Elriges）。

• 发出信息对象的名字是艾贝·斯莱尼（Abe·Slaney）。

1.4.2. 古典方法

古典方法指的是在经验事实的基础上，对事件 \(A\) 的可能性进行逻辑分析后得出该事件的概率。其基本思想为所设计的随机现象只有有限个样本点，设为 \(n\) 个。每个样本点发生的可能性相等（称等可能性）。若事件 \(A\) 含有 \(k\) 个样本点，则事件 \(A\) 的概率为：

\[ P(A) = \frac{k}{n} \]

Example 1.5 (抛硬币)

投掷两枚硬币，如何求出现一正一反的概率？

Solution

样本空间为 \(\Omega= \{\text{(正,正),(正,反),(反,正),(反,反)} \}\) 。于是，样本空间 \(\Omega\) 共有 \(4\) 个样本点。事件“出现一正一反”含有的样本点的个数为 \(2\) 。因此，所求的概率为 \(1/2\) 。

古典方法是概率轮发展初期确定概率的常用方法，所得的概率又称为古典概率。在古典概率的计算中，经常使用排列组合工具。排列组合本质上都是计算“从 \(n\) 个元素中任取 \(r\) 个元素”的取法数量。组合不讲究取出元素间的次序，而排列讲究取出元素间的次序。常用的排列、组合有有以下四种：

排列

从 \(n\) 个不同的元素中任取 \(r(r\leq n)\) 个元素拍成一列（考虑元素先后出现次序）。这种排列数为：

\[ P_n^r = n\times (n-1)\times \cdots \times (n-r+1) = \frac{n!}{(n-r)!}.\]

特别地， \(r=n\) 时，称 \(P_n^n = n!\) 为全排列。

重复排列

从 \(n\) 个不同元素中每次去处一个，放回后在取下一个，如此连续取 \(r\) 次所得的排列。这种重复排列数共有 \(n^r\) 个。注意：这里允许 \(r>n\) 。

组合

从 \(n\) 个不同元素中任取 \(r(r\leq n)\) 个元素并成一组（不考虑元素间的先后次序）。这种组合数为：

\[\begin{split} C_n^r = \begin{pmatrix}n\\r\end{pmatrix}= \frac{n!}{r!(n-r)!} \end{split}\]

特别的组合数有：

• \(0!=1\) ；

• \(C_n^0 = 1\) ；

• \(C_n^r= C_n^{n-r}\)

重复组合

从 \(n\) 个不同元素中每次取出一个，然后放回后再取下一个。如此连续取 \(r\) 次所得的组合。这种重复组合数为：

\[\begin{split} \begin{pmatrix}n+r-1\\r\end{pmatrix} \end{split}\]

重复组合数的计算方式为：总共有 \(n\) 个元素，设为共有 \(n\) 个盒子，我们用 \(n+1\) 根棒子做间隔。如果第 \(i\) 个元素取到过一次，就标记一个“〇”。需要考虑重复组合数，除了不可动的头尾两根棒子之外，余下的棒子和盒子可以随意放置，于是，相当于在 \(n+r-1\) 个位置上任取 \(r\) 个放“〇”。因此，重复组合数为：

\[\begin{split} \begin{pmatrix}n+r-1\\r\end{pmatrix} = \begin{pmatrix}n+r-1\\ n-1\end{pmatrix} \end{split}\]

Example 1.6 (不放回抽样)

设有 \(N\) 件产品，其中 \(M\) 件不合格品和 \(N-M\) 件合格品，从中不放回地抽出 \(n\) 件。求事件 \(A_m=\) “所抽出的产品中有 \(m\) 件不合格品” 的概率。

Solution

从 \(N\) 件产品中，不放回地抽取 \(n\) 件产品，组合数为：

\[ C_N^n \]

而抽到 \(m\) 件不合格品，表示抽到 \(n-m\) 件产品是合格品，组合数为：

\[ C_M^m \times C_{N-M}^{n-m} \]

于是， \(A_m\) 的概率为：

\[ P(A_m) = \frac{C_M^m \cdot C_{N-M}^{n-m}} {C_N^n}, m = 0,1,\cdots,\min\{M,n\} \]

Example 1.7 (有放回抽样)

设有 \(N\) 件产品，其中 \(M\) 件不合格品和 \(N-M\) 件合格品，从中有放回地抽出 \(n\) 件。求事件 \(B_m=\) “所抽出的产品中有 \(m\) 件不合格品” 的概率。

Solution

从 \(N\) 件产品中，有放回地抽取 \(n\) 件产品，重复排列数为：

\[ N^{n} \]

所抽到的产品中有 \(m\) 件不合格品，这就表示抽到 \(n-m\) 件产品是合格品。从 \(N-M\) 件合格品中，有放回地抽取了 \(n-m\) 次；从 \(M\) 件不合格品中，有放回地抽取了 \(m\) 次。于是共有 \(M^{m} (N-M)^{n-m}\) 种取法。再考虑所取到的 \(m\) 件不合格品可能出现在 \(n\) 次中的任何 \(m\) 次抽取中得到，总共有 \(C_n^m\) 种可能。所以事件 \(B_m\) 含有：

\[ C_n^m M^{m} (N-M)^{n-m} \]

个样本点。

于是， \(B_m\) 的概率为：

\[ P(B_m) = \frac{C_n^m M^{m} (N-M)^{n-m}} {N^n}, m = 0,1,\cdots,n \]

Remark 1.4

注意到： \(P(B_m)\) 可以改写为：

\[\begin{eqnarray*} P(B_m) &=& \frac{C_n^m M^{m} (N-M)^{n-m}} {N^n} \\ &=& C_n^m\left(\frac{M}{N}\right)^{m} \left(1-\frac{M}{N}\right)^{n-m} \end{eqnarray*}\]

令 \(M/N = p\) 。于是：

\[ P(B_m) = C_n^m \left(p\right)^{m} \left(1-p\right)^{n-m} \]

1.4.3. 几何方法

在几何方法中，一个随机现象的样本空间 \(\Omega\) 充满某个区域，其度量（长度、面积或提及）大小用 \(S_{\Omega}\) 表示。任意一点落在度量相同的子区域内（可能位置不同）是等可能的。若事件 \(A\) 为 \(\Omega\) 中某个子区域，且其度量大小可用 \(S_A\) 表示，则事件 \(A\) 的概率为：

\[ P(A) = \frac{S_A}{S_{\Omega}} \]

Example 1.8 (会面问题)

甲乙两人约定下午6点到7点之间在某处会面，并约定先到者应等候另一个人20分钟，过时即可离去。求两人能会面的概率。

Solution

设 \(x\) 和 \(y\) 分别表示甲和乙到达约会地点的时间点。甲乙两人到达的时间介于6点至7点间。令 \(x\) 和 \(y\) 都是在区间 \([0,60]\) 之间取值。 甲乙两人能会面，意味着甲乙到达时间差不超过20分钟，即 \(|x-y| \leq 20\) 。

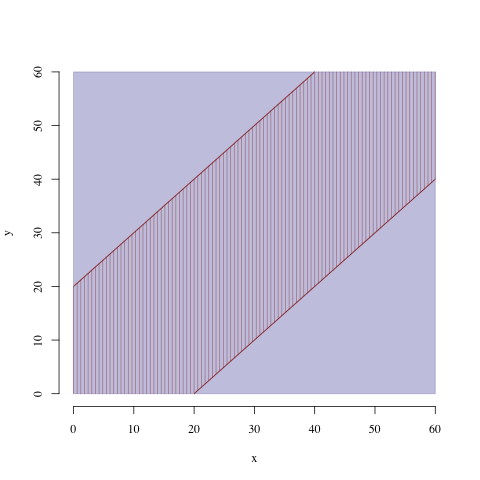
Fig. 1.2 甲乙两人会面的示意图

根据题意，我们可以绘制一张图。图中蓝色区域是甲乙两人到达的时间的所有样本点，即样本空间 \(\Omega\) ，而甲乙两人能够会面的时间点在红色斜线的区域，记为 \(A\) 。 于是，计算图中对应的面积来得到概率，即：

\[\begin{eqnarray*} S_{\Omega} &=& 60^2 = 3600\\ S_A &=& 3600 - 2 \times \frac{1}{2} \times 40^2= 2000\\ P(A) &=& \frac{S_A}{S_{\Omega}} = \frac{2000}{3600} = \frac{5}{9} \end{eqnarray*}\]

此外，可以观看专题精讲——“蒲丰投针”了解更多几何方法。