4.1. 概率分布列#
- 概率分布列
设 \(X\) 是一个离散随机变量,如果 \(X\) 的所有可能取值 \(x_1,x_2,..,x_n,...,\) 则称 \(X\) 取 \(x_i\) 的概率
为X的概率分布列,或称概率质量函数(P.M.F)。
通常,我们会将概率分布列写出一个表格的形式,见 Table 4.1。
\(X\) |
\(x_1\) |
\(x_2\) |
\(\cdots\) |
\(x_n\) |
\(\cdots\) |
\(P\) |
\(p_1\) |
\(p_2\) |
\(\cdots\) |
\(p_n\) |
\(\cdots\) |
Example 4.1
掷两颗骰子,其样本空间含有 \(36\) 个样本点 \(\Omega=\{(x, y): x, y=1,2, \ldots, 6\}\) 。在 \(\Omega\) 上我们定义 \(3\) 个随机变量 \(X,Y,Z\) 。
\(X\) 为两颗骰子的点数之和,则其分布列为
\(X\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
\(10\) |
\(11\) |
\(12\) |
\(P\) |
\(1/36\) |
\(1/18\) |
\(1/12\) |
\(1/9\) |
\(5/36\) |
\(1/6\) |
\(5/36\) |
\(1/9\) |
\(1/12\) |
\(1/18\) |
\(1/36\) |
\(Y\) 为 \(6\) 点的骰子个数,则其分布列为
\(Y\) |
\(0\) |
\(1\) |
\(2\) |
\(P\) |
\(25/36\) |
\(10/36\) |
\(1/36\) |
\(Z\) 为最大点数,则其分布列为
\(Z\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(P\) |
\(1/36\) |
\(3/36\) |
\(5/36\) |
\(7/36\) |
\(9/36\) |
\(11/36\) |
Theorem 4.1
任一概率分布列 \(\{p_i\}\) 都具有如下两条基本性质:
非负性: \(p(x_i) \geq 0, i=1,2,\cdots\) ;
正则性: \(\sum_{i=1}^{\infty} p(x_i) = 1\) 。
Remark 4.1
以上两条基本性质也是判断某个函数是否为随机变量的概率分布列的依据。
Question
分布函数与分布列有什么关系?
Example 4.2
设离散随机变量 \(X\) 的分布列为:
\(X\) |
\(-1\) |
\(2\) |
\(3\) |
\(P\) |
\(0.25\) |
\(0.5\) |
\(0.25\) |
求:
\(P(X\leq 0.5)\) ;
\(P(1.5< X\leq 2.5)\) ;
写出 \(X\) 的分布函数。
Solution
根据定义可知:
根据定义可知:
根据分布函数与分布列的关系可知:
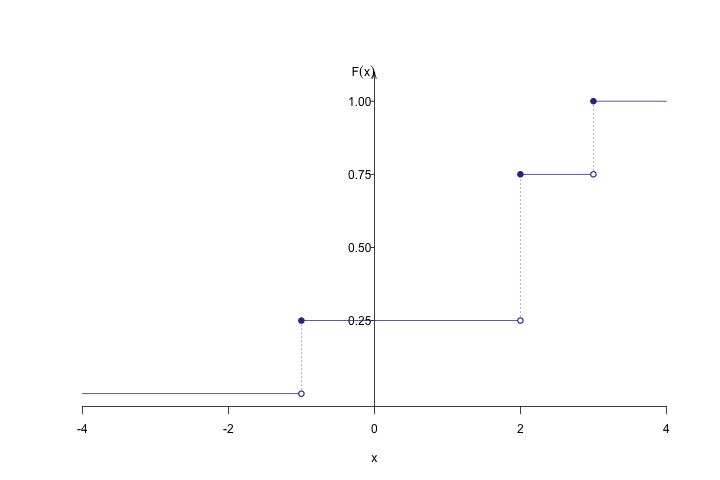
当 \(x<-1\) 时, \(F(x) = P(X\leq x) = 0\) .
当 \(-1 \leq x < 2\) 时, \(F(x) = P(X\leq x) = P(X = -1) = 0.25\) .
当 \(2 \leq x < 3\) 时, \(F(x) = P(X\leq x) = P(X = -1) + P(X=2)= 0.75\) .
当 \(x \geq 3\) 时, \(F(x) = P(X\leq x) = P(X = -1) + P(X=2) + P(X=3)= 1\) .
综上,分布函数为
Summary
对于离散型随机变量,通过其密度分布列来判断其分布类型。