14.1. 引导问题

根据分布的可加性，我们知道卡方分布是具备可加性的。具体来说，若 \(X_i\) 是独立同分布的卡方分布随机变量，即 \(X_i \sim \chi^2(1)\) 。于是，

\[ \begin{eqnarray*} S_{k} = \sum_{i=1}^{k}X_i \sim \chi^2(k) \end{eqnarray*} \]

我们考虑 1 个、2 个、10 个以及 30 个随机变量之和的密度函数见图 Fig. 14.1 。

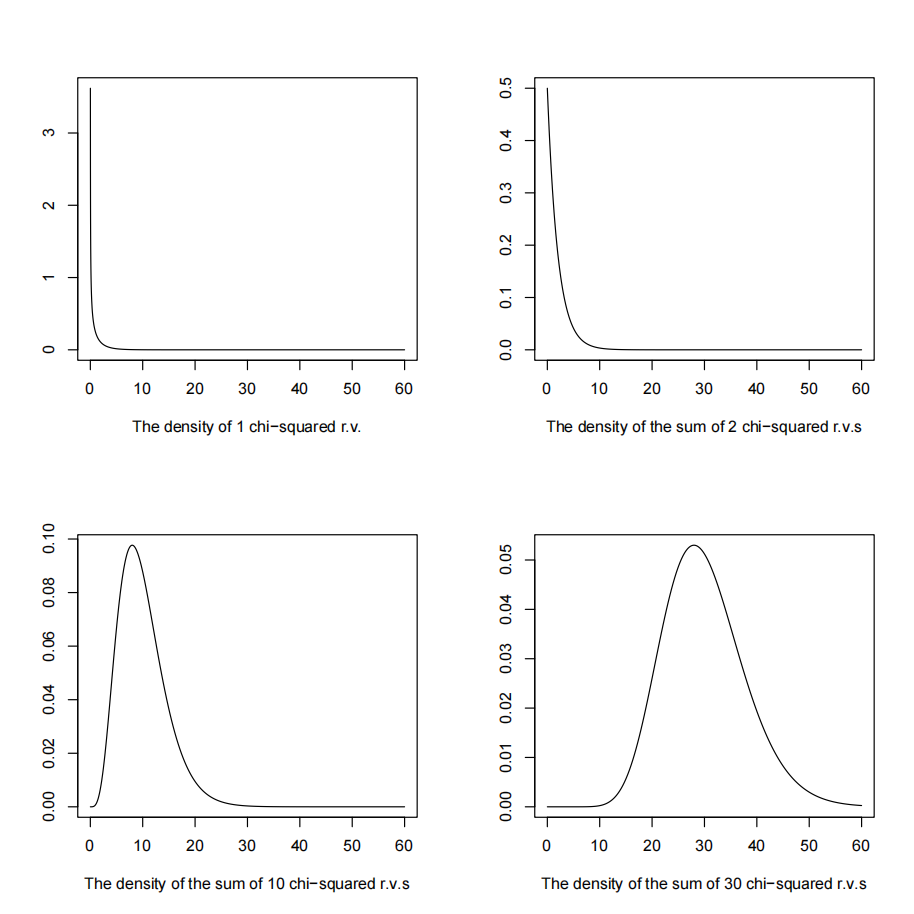
Fig. 14.1 多个卡方分布之和的密度函数

Remark

随着 \(k\) 的增加， \(S_k\) 的密度函数图像越来越接近正态分布曲线。

对于卡方分布 \(\chi^2(k)\) 而言，其期望和方差分别为

\[ E(S_k)=k, \quad \text{Var}(S_k) = 2k.\]

当 \(k\) 增加时， \(S_k\) 的密度函数的位置右移，且 \(p_{k}(s)\) 的方差也增大。这意味着这个分布的中心趋向 \(\infty\) ，其方差也趋向 \(\infty\) ，分布极不稳定。因此，直接讨论 \(S_k\) 的分布是有困难的。于是，在中心极限定理的研究中均对 \(S_k\) 进行标准化，即

\[ S_k^\ast = \frac{S_k - E(S_k)}{\sqrt{\text{Var}(S_k)}} \]

可以证明

\[\begin{split} \begin{eqnarray*} E(S_k^\ast) = 0\\ \text{Var}(S_k^\ast) = 1 \end{eqnarray*} \end{split}\]

一个很自然的问题是 \(S_k^{\ast}\) 的极限分布是否为标准正态分布 \(N(0,1)\) ?

Question

中心极限定理本身研究的是在什么条件下，随机变量之和的极限分布是正态分布。