5.1. 引导问题：对于早八点的课程，学生何时能到教室？

Example 5.1

我们想要研究：上早八课程的学生一般什么时候会到教室。记学生到达教室的时刻为 \(X\) 。 \(X\) 表示 \(7\) 点后的分钟数，显然是一个随机变量。共采集了 \(83\) 名学生的打卡时间。我们分别按 \(1\) 分钟间隔、 \(2\) 分钟间隔、 \(5\) 分钟间隔和 \(10\) 分钟间隔绘制了直方图，如图 Fig. 5.1。学生大部分在 \(40\) 分到 \(55\) 分之间到达教室，一小部分学生会提前 \(20\) 分钟到达教室，还有一部分学生倾向于临近 \(8\) 点才到。

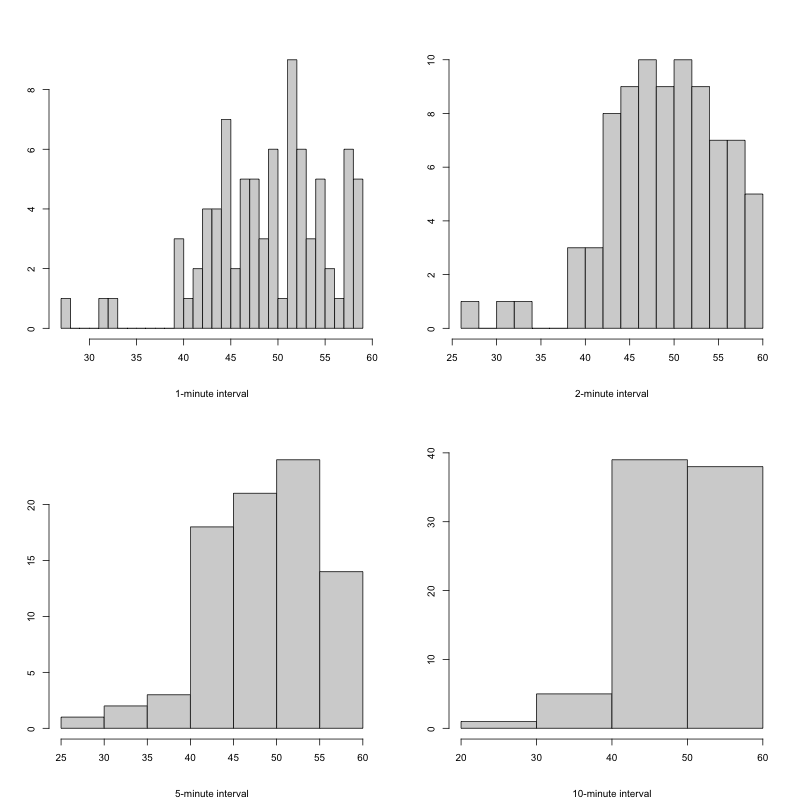
Fig. 5.1 学生到达教室的直方图

Hint

我们发现，时间是连续的，且 \(X\) 的取值可以充满 \((0,60)\) 这个区间。于是， \(X\) 就是一个连续型随机变量。当我们不断细化间隔的划分，在同一时刻到达教室的学生不会超过 \(1\) 人。于是，利用概率分布列 \(P(X=x)\) 来刻画 \(X\) 是不恰当的。所以，我们需要提出一个新的概念——概率密度函数。