16.4. 常见统计量：样本矩

假定在样本 \(x_1,x_2,\cdots,x_n\) 中有 \(k\) 个不同的取值 \(a_1,a_2,\cdots,a_k\) 。每一个样本 \(x_i\) 来自于一个均值为 \(\mu\) 和方差为 \(\sigma^2\) 分布的随机变量。

数据	\(a_1\)	\(a_2\)	\(\cdots\)	\(a_k\)
频数	\(m_1\)	\(m_2\)	\(\cdots\)	\(m_k\)
频率	\(\frac{m_1}{n}\)	\(\frac{m_2}{n}\)	\(\cdots\)	\(\frac{m_k}{n}\)

Remark

\(\sum_{i=1}^{k} m_{i}=n ,\sum_{i=1}^{k} a_{i} m_{i}=\sum_{i=1}^{n} x_{i}\) 。

因为 \(F_n(x)\) 是一个某个随机变量的分布函数，假定该随机变量为 \(X\) ，所以，

\[\begin{split} \begin{eqnarray*} E_{F_{n}}(X) &=&\sum_{i=1}^{k} a_{i} \cdot \frac{m_{i}}{n}=\frac{1}{n} \sum_{i=1}^{k} a_{i} m_{i}=\frac{1}{n} \sum_{i=1}^{n} x_{i} \\ E_{F_{n}}\left(X^{l}\right) &=&\sum_{i=1}^{k} a_{i}^{l} \frac{m_{i}}{n}=\frac{1}{n} \sum_{i=1}^{k} a_{i}^{l} m_{i}=\frac{1}{n} \sum_{i=1}^{n} x_{i}^{l} \end{eqnarray*} \end{split}\]

\[\begin{split} \begin{eqnarray*} \text{Var}_{F_{n}}(X) &=&\sum_{i=1}^{k}\left(a_{i}-E_{F_{n}}(X)\right)^{2} \cdot \frac{m_{i}}{n} \\ &=&\sum_{i=1}^{k}\left(a_{i}-\bar{x}\right)^{2} \cdot \frac{m_{i}}{n} \\ &=&\frac{1}{n} \sum_{i=1}^{k}\left(a_{i}-\bar{x}\right)^{2} \cdot m_{i} \\ &=&\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \end{eqnarray*} \end{split}\]

Remark

我们通常记 \(\bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_{i}\) ，而 \(s_{n}^2 = \frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\) 。

样本 \(k\) 阶中心距

设 \(x_1,x_2,\cdots,x_n\) 是样本， \(k\) 为正整数，则统计量

\[ a_k = \frac{1}{n} \sum_{i=1}^n x_i^k \]

称为样本 \(k\) 阶原点矩；统计量

\[ b_k = \frac{1}{n} \sum_{i=1}^n (x_i-\bar{x})^k \]

称为样本 \(k\) 阶中心矩。

Remark

样本一阶原点矩是样本均值；样本二阶中心矩是样本方差。

16.4.1. 样本均值

样本均值 \(\bar{x}\) 是最简单的统计量。首先考察其期望和方差。我们可以证明

\[\begin{split} \begin{eqnarray*} E(\bar{x}) &=& E\left( \frac{1}{n}\sum_{i=1}^{n} x_{i} \right) = \frac{1}{n}\sum_{i=1}^{n} E(x_{i}) = \mu \\ \text{Var}(\bar{x}) &=& \text{Var} \left( \frac{1}{n}\sum_{i=1}^{n} x_{i} \right) = \frac{1}{n^2}\sum_{i=1}^{n} \text{Var}(x_{i}) = \frac{\sigma^2}{n}. \end{eqnarray*} \end{split}\]

其次，我们考虑 \(\bar{x}\) 的分布。

• 精确分布：如果 \(x_{1}, x_{2}, \ldots, x_{n}\) 均来自正态分布 \(N\left(\mu, \sigma^{2}\right)\) ，那么 \(\bar{x}\) 的分布是 \(N(\mu,\sigma^2/n)\) 。

• 近似分布 1（渐近分布）：如果 \(x_{1}, x_{2}, \ldots, x_{n}\) 均来自未知分布 \(\Pi\left(\mu, \sigma^{2}\right)\) ，那么，根据 CTL，

\[ \frac{\bar{x}-E(\bar{x})}{\sqrt{{\text{Var}}(\bar{x})}} \stackrel{L}{\longrightarrow} N(0,1). \]

• 近似分布 2（蒙特卡洛分布）：如果 \(x_{1},x_{2},\cdots,x_{5}\) 来自于指数分布 \(Exp(1/5)\) ，那么 \(\bar{x} = \frac{1}{5}\sum_{i=1}^5x_i\) 的蒙特卡洛分布应如图 Fig. 16.1 所示。图中直方图刻画的是 \(\bar{x}\) 的蒙特卡洛分布，而红线表示的是其真实的密度函数。

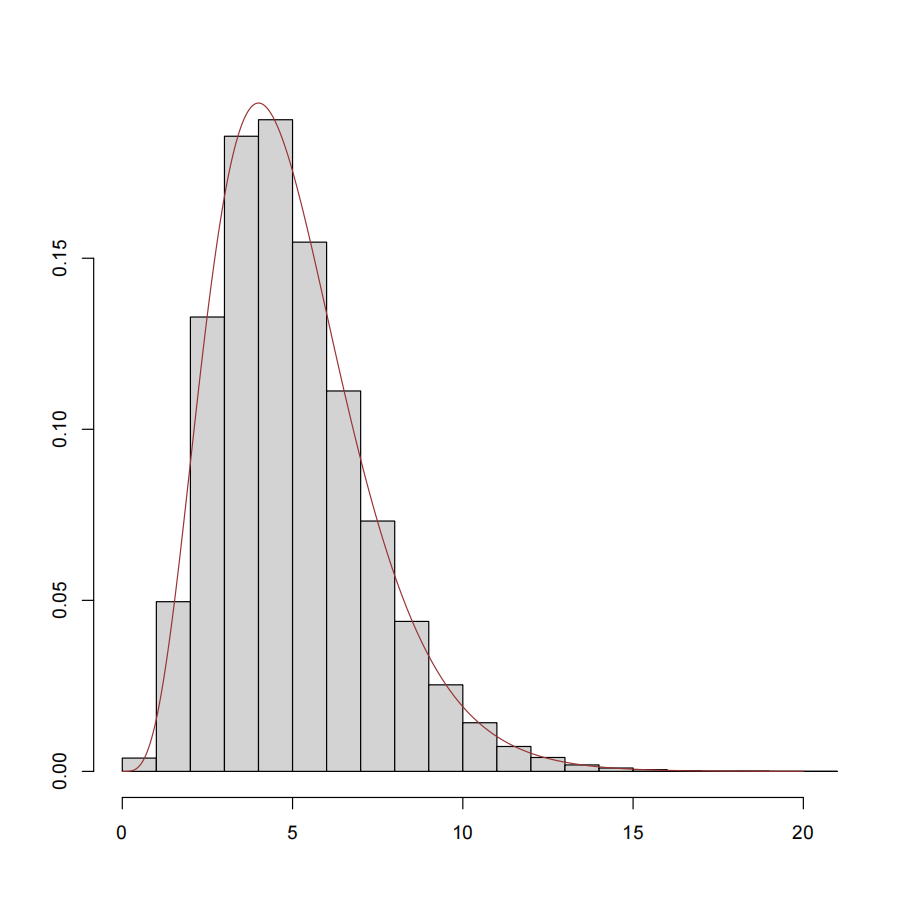
Fig. 16.1 蒙特卡洛分布

在实现蒙特卡洛分布时，只需要进行以下三步：

• 从指数分布 \(Exp(1/5)\) 产生 \(5\) 个随机数： \(x_1^{m},x_2^{m},,\cdots,x_5^{m}\) ；

• 计算 \(\bar{x}^{m} = \frac{1}{5}\sum_{i=1}^5x_i^{m}；\)

• 重复前面两步 \(M\) 次。

由此可以得到 \(M\) 个样本均值的取值，来得到其经验分布函数。

Question

如何保留蒙特卡洛分布的信息？

Question

请问 \(\bar{x}\) 的真实分布是什么？

16.4.2. 样本方差和样本标准差

样本方差 \(s_{n}^2\) 也是一种常用的统计量。为了考虑 \(s_{n}^2\) 的期望，我们可以计算偏差平方和 \(\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\) 的期望，即

\[\begin{split} \begin{eqnarray*} E\left( \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\right) &=& E\left(\sum_{i=1}^{n}\left(x_{i}^{2}-2 x_{i} \bar{x}+\bar{x}^{2}\right)\right) \\ &=& E\left(\sum_{i=1}^{n} x_{i}^{2}-2 n \bar{x}^{2}+n \bar{x}^{2}\right) \\ &=& E\left(\sum_{i=1}^{n} x_{i}^{2}-n \bar{x}^{2}\right) \\ &=&\left(\sum_{i=1}^{n} E\left(x_{i}^{2}\right)-n E\left(\bar{x}^{2}\right)\right) \\ &=&\left[\sum_{i=1}^{n}\left(\text{Var}\left(x_{i}\right)+E^2\left(x_{i}\right)\right)-n\left(E^{2}(\bar{x})+\text{Var}(\bar{x})\right)\right] \\ &=& \cdot\left(n \cdot\left(\sigma^{2}+\mu^{2}\right)-n\left(\mu^{2}+\frac{\sigma^{2}}{n}\right)\right) \\ &=&(n-1) \sigma^{2} \end{eqnarray*} \end{split}\]

因此，我们发现 \(E(s_n^2) = (n-1)\sigma^2/n \neq \sigma^2\) 。在实际中，我们常采用

\[ \frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \]

作为样本方差。而定义样本标准差为 \(s = \sqrt{s^2}\) 。

16.4.3. 样本偏度和样本峰度（选修）

样本偏度和样本峰度

设 \(x_1,x_2,\cdots,x_n\) 是样本，则称统计量

\[ \hat{\beta}_s = \frac{b_3}{b_2^{3/2}} \]

为样本偏度； 称统计量

\[ \hat{\beta}_k = \frac{b_4}{b_2^2} - 3 \]

为样本峰度。