3.1. 随机变量的定义

随机变量

设 \((\Omega,\mathcal{F},P)\) 为某一随机现象的概率空间， \(X\) 是定义在 \(\Omega\) 上的实值函数，则 \(X\) 是一个随机变量当且仅当对任意的实数 \(x\) ，

\[ \{\omega \in \Omega: X(\omega) \leq x\} \in \mathcal{F} \]

通常用大写字母 \(X,Y,Z\) 表示随机变量，其取值用小写字母 \(x,y,z\) 等表示。

Example 3.1

考虑抛一枚硬币三次的结果。记硬币正面朝上为“1”，而硬币反面朝上为“0”。我们考虑样本空间及硬币正面朝上的次数。

Table 3.1 抛三枚硬币的结果

抛三次硬币的结果	正面朝上的次数 \(X\)
\(\omega_1 = (\text{反, 反, 反})\)	0
\(\omega_2 = (\text{正, 反, 反})\)	1
\(\omega_3 = (\text{反, 正, 反})\)	1
\(\omega_4 = (\text{反, 反, 正})\)	1
\(\omega_5 = (\text{正, 正, 反})\)	2
\(\omega_6 = (\text{正, 反, 正})\)	2
\(\omega_7 = (\text{反, 正, 正})\)	2
\(\omega_8 = (\text{正, 正, 正})\)	3

这里，一枚硬币抛三次，正面朝上的次数就是所定义的随机变量。

Remark 3.1

• 不同的样本点对应不同的实数；

• 多个样本点对应同一个实数；

• 样本点可以用数值表示，也可以不用数值表示；但随机变量一定是数值型；

Example 3.2

在一个周长为 \(1\) 的轮盘中，中心有一个指针，并标记一个点为“ \(0\) ”。我们旋转指针，记指针在轮盘停留的位置与“ \(0\) ”点按逆时针测量的弧长为 \(X\) ，如图 Fig. 3.1。这里 \(X\) 也是一个随机变量。

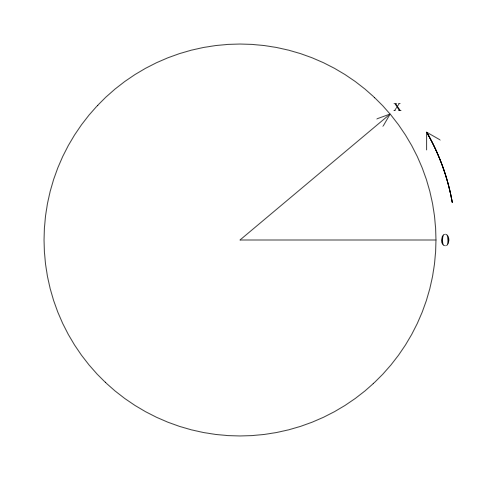
Fig. 3.1 轮盘

Summary

随机变量 \(X\) 本质上从 \((\Omega,\mathcal{F})\) 到 \((R,\mathcal{B})\) 的可测映射。这里涉及测度论的内容，超出了本课程的内容范围。