8.5. 联合分布列与边际分布列

联合分布列

如果二维随机变量 \((X,Y)\) 只取有限个或可列个数对 \(\left(x_{i}, y_{i}\right)\) 则称 \((X,Y)\) 为二维离散随机变量，称

\[p_{i j}=P\left(X=x_{i}, Y=y_{j}\right) \quad i, j=1.2, \cdots\]

为 \((X,Y)\) 的联合分布列。

Property 8.1

联合分布列的基本性质：

• 非负性: \(p_{ij}\geq 0\) ;

• 正则性: \(\sum_{i=1}^{\infty}\sum_{j=1}^{\infty} p_{ij} = 1\) .

边际分布列

如果二维随机便利 \((X,Y)\) 的联合分布列 \(\{P(X=x_i,Y=y_j)\}\) 中，称

\[ P(X=x_i) = \sum_{j=1}^\infty P(X=x_i,Y=y_j) , i =1,2,\cdots \]

为 \(X\) 的边际分布列。类似地，称

\[ P(Y=y_j) = \sum_{i=1}^\infty P(X=x_i,Y=y_j) , j =1,2,\cdots \]

为 \(Y\) 的边际分布列。

Remark

我们通常采用表格的形式来表示联合分布列和边际分布列，即

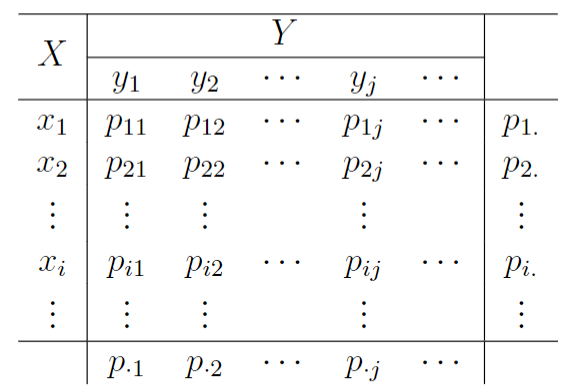
Fig. 8.2 联合分布列与边际分布列

• 联合分布列： \(p_{ij} = P(X=x_i,Y=y_j)\) ;

• 边际分布列： \(p_{i\cdot} = P(X=x_i)\) ， \(p_{\cdot j} = P(Y=y_j)\) 。

8.5.1. 联合密度函数

联合密度函数

如果存在二元非负函数 \(p(x,y)\) ，使得二维随机变量 \((X,Y)\) 的分布函数 \(F(x,y)\) 可表示为

\[F(x, y)=\int_{-\infty}^{x} \int_{-\infty}^{y} p(u, v) \text{d} v \text{d} u\]

则称 \((X,Y)\) 为二维连续随机变量，称 \(p(x,y)\) 为 \((X,Y)\) 的联合密度函数。

Remark

• 在 \(F(X,Y)\) 偏导数存在的点上有

\[p(x, y)=\frac{\partial^{2}}{\partial x \partial y} F(x, y) .\]

• 给定联合密度函数 \(p(x,y)\) ，若 \(G\) 为平面上的一个区域，则事件 \(\{(X,Y)\in G\}\) 的概率可以表示为 \(G\) 上对 \(p(x,y)\) 的二重积分

\[ P((X,Y) \in G) = \underset{(x,y)\in G}{\iint} p(x,y)\text{d} y \text{d} x. \]

Example 8.4

设 \((X,Y)\) 的联合密度函数为

\[\begin{split} p(x,y) = \left\{ \begin{aligned} & 6 e^{-2x - 3y}, & x>0,y>0\\ &0 , & \text{其他}. \end{aligned} \right. \end{split}\]

求：

• \(P(X<1,Y>1)\) ；

• \(P(X>Y)\) 。

Solution

• 我们知道 \(P(X<1,Y>1)\) 为

\[\begin{split} \begin{eqnarray*} P(X<1,Y>1) &=&= \int_{1}^{\infty}\int_{0}^1 6 e^{-2x - 3y} \text{d}x \text{d}y\\ &=& 6\cdot \int_{0}^1 e^{-2x}\text{d}x \cdot \int_{1}^{\infty} e^{-3y}\text{d}y\\ &=& (1-e^{-2})e^{-3}. \end{eqnarray*} \end{split}\]

• 我们知道 \(P(X>Y)\) 为

\[\begin{split} \begin{eqnarray*} P(X>Y) &=&= \int_{0}^{\infty}\int_{y}^\infty 6 e^{-2x - 3y} \text{d}x \text{d}y\\ &=& 6\int_{0}^{\infty}e^{- 3y} \int_{y}^\infty e^{-2x } \text{d}x \text{d}y\\ &=& \int_{0}^{\infty}3e^{- 3y}e^{-2y}\text{d}y\\ &=& 3/5. \end{eqnarray*} \end{split}\]

Property 8.2

联合密度函数的基本性质：

• 非负性： \(p(x,y)\geq 0\) ；

• 正则性： \(\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} p(x,y) \text{d}y\text{d}x = 1\) 。

边际密度函数

如果二维连续随机变量 \((X,Y)\) 的联合密度函数为 \(p(x,y)\) ，称

\[p_X(x) = \int_{-\infty}^{\infty} p(x,y) \text{d}y\]

为 \(X\) 的边际密度函数。类似地，称

\[p_Y(y) = \int_{-\infty}^{\infty} p(x,y) \text{d}x\]

为 \(Y\) 的边际密度函数。

Example 8.5

设二维随机变量 \((X,Y)\) 的联合密度函数为

\[\begin{split} p(x,y) = \left\{ \begin{aligned} &1, &0 <x<1, |y|<x\\ &0, &\text{其他}. \end{aligned} \right. \end{split}\]

求：

• 边际密度函数 \(p_X(x)\) 和 \(p_Y(y)\) ；

• \(P(X<1/2)\) 和 \(P(Y>1/2)\) 。

Solution

• 对于任意 \(0<x<1\) ，边际密度函数 \(p_X(x)\) 为

\[\begin{split} \begin{eqnarray*} p_X(x) &=& \int_{-\infty}^{\infty} p(x,y) \text{d}y\\ &=& \int_{-x}^{x} 1 \text{d}y\\ &=& 2x. \end{eqnarray*} \end{split}\]

对于任意 \(-1<y<0\) ，边际密度函数 \(p_Y(y)\) 为

\[\begin{split} \begin{eqnarray*} p_Y(y) &=& \int_{-\infty}^{\infty} p(x,y) \text{d}x\\ &=& \int_{-y}^{1} 1 \text{d}x\\ &=& 1+y. \end{eqnarray*} \end{split}\]

对于任意 \(0<y<1\) ，边际密度函数 \(p_Y(y)\) 为

\[\begin{split} \begin{eqnarray*} p_Y(y) &=& \int_{-\infty}^{\infty} p(x,y) \text{d}x\\ &=& \int_{y}^{1} 1 \text{d}x\\ &=& 1-y. \end{eqnarray*} \end{split}\]

综上， \(X\) 的边际密度函数 \(p_X(x)\) 为

\[\begin{split} p_X(x) = \left\{\begin{aligned} & 2x, & 0<x <1 \\ &0 , & \text{其他}. \end{aligned} \right. \end{split}\]

而 \(Y\) 的边际密度函数 \(p_Y(y)\) 为

\[\begin{split} p_Y(y) = \left\{\begin{aligned} & 1-|y|, & -1<y <1 \\ &0 , & \text{其他}. \end{aligned} \right. \end{split}\]

• 根据 \(p_X(x)\) 和 \(p_Y(y)\) 可知， \(P(X<1/2)\) 为

\[ P(X<1/2) = \int_{0}^{1/2}2x \text{d}x = 1/4. \]

而 \(P(Y>1/2)\) 为

\[ P(Y>1/2) = \int_{1/2}^{1}1-|y| \text{d}y = 1/8. \]