2.2. 条件概率的定义

条件概率

设 \(A\) 与 \(B\) 是样本空间 \(\Omega\) 中的两个事件，若 \(P(B)> 0\) ，则称

\[P(A|B)=\frac{P(AB)}{P(B)} \]

为“在事件 \(B\) 条件下，事件 \(A\) 的条件概率”，简称条件概率，记作 \(P(A|B)\) 。

Example 2.1

投掷一颗公平的四面骰子两次。令 \(X\) 表示第一次投掷的结果， \(Y\) 表示第二次投掷的结果。若：

\[ A_m = \{\max\{X,Y\} = m\}, \quad B = \{\min\{X,Y\} = 2\} \]

求条件概率 \(P(A_m|B)\) ，其中 \(m=1,2,3,4\) 。

Solution

根据条件概率的定义可知，

\[ P(A|B) = \frac{P(A\cap B)}{P(B)} \]

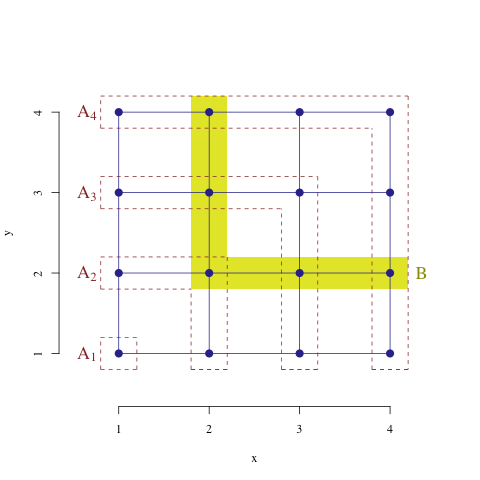
Fig. 2.1 投掷两次四面骰子的结果

在Fig. 2.1中，蓝色的点表示16种结果，黄色的区域表示事件 \(B = \{\min\{X,Y\} = 2\}\) ，红色虚线框住的区域分别表示事件 \(A_m = \{\max\{X,Y\} = m\}\) 。 \(A_1\) 与 \(B\) 的交集为空， \(A_2\) 与 \(B\) 的交集只有一个元素，而 \(A_m\) 与 \(B\) 的交集有两个元素， \(m=3,4\) 。

于是，我们有

\[\begin{split} P(A_m | B) = \left\{ \begin{aligned} & 2/5, &m= 3\text{或}4\\ & 1/5, & m= 2\\ & 0, & m= 1 \end{aligned} \right. \end{split}\]

Question

条件概率 \(P(A|B)\) 本质上是给定 \(B\) 的条件下，事件 \(A\) 的概率。那么 \(P(\cdot|B)\) 是否满足概率的性质？

Theorem 2.1

条件概率是概率，即若设 \(P(B)>0\) ，则

• \(P(A|B) \geq 0, A \in \mathcal{F}\) ；

• \(P(\Omega|B) =1\) ；

• 若 \(\mathcal{F}\) 中的 \(A_1,A_2,\cdots,A_n,\cdots,\) 互不相容，则

\[ P\left(\cup_{n=1}^{\infty} A_n |B \right) = \sum_{n=1}^{\infty} P(A_n | B) \]

Proof

在条件概率的定义中，假定存在一个概率空间 \((\Omega,\mathcal{F},P)\) 。给定随机事件 \(B\) ， \(P(B)>0\) 。 根据概率的公理化定义，需要论证条件概率满足非负性、正则性和可列可加性。

• 对于任意一个随机事件 \(A\in \mathcal{F}\) ， \(P(AB)\geq 0\) ，则 \(P(A|B)\geq 0\) 。

• 对于必然事件 \(\Omega\) ，有：

  \[ P(\Omega ) = \frac{P(\Omega \cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1 \]

• 对于一列互不相容的随机事件 \(A_1,A_2,\cdots,A_n,\cdots \in \mathcal{F}\) ，有：

  \[\begin{eqnarray*} P\left( \cup_{i=1}^{\infty} A_i | B\right) &=& \frac{P\left( \left(\cup_{i=1}^{\infty} A_i\right) \cap B \right)}{P(B)} \\ &=& \frac{P\left( \cup_{i=1}^{\infty}\left( A_i \cap B \right) \right)}{P(B)} \\ &=& \frac{ \sum_{i=1}^{\infty} P\left(\left( A_i \cap B \right) \right)}{P(B)} \\ &=& \sum_{i=1}^{\infty} P\left(A_i | B \right) \end{eqnarray*} \]