12.2. 依概率收敛

我们举一个例子，可以直观感受一下随机变量序列是可以收敛的。

Example 12.1

在抛一枚均匀硬币（正面反面出现的概率相等）的场景下，令随机变量 \(X_i\) 表示 \(i\) 枚硬币正面朝上的频率。考虑一次实验的数据，如表 Table 12.1 。

Table 12.1 10 次抛硬币的结果

第 \(i\) 次抛硬币	1	2	3	4	5	6	7	8	9	10
结果	反面	反面	正面	正面	反面	正面	正面	正面	反面	反面

于是，根据抛硬币的结果，随机变量序列 \(\{X_i\}\) 的取值为 \(x_i\) ，见表 Table 12.2

Table 12.2 随机变量序列的取值情况

\(x_i\)	1	2	3	4	5	6	7	8	9	10
取值	\(0\)	\(0\)	\(0.33\)	\(0.50\)	\(0.40\)	\(0.50\)	\(0.57\)	\(0.63\)	\(0.56\)	\(0.50\)

根据表 Table 12.2 ，我们可以将 \(\{X_i\}\) 绘制在一张图中，如图 Fig. 12.1 。

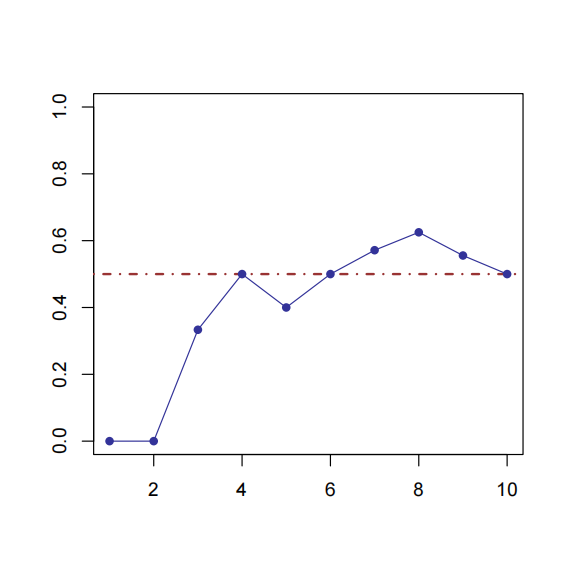
Fig. 12.1 抛 10 枚硬币的结果

类似地，我们分别抛 30、60、90 以及 120 次硬币后的结果，如图 Fig. 12.2 所示。

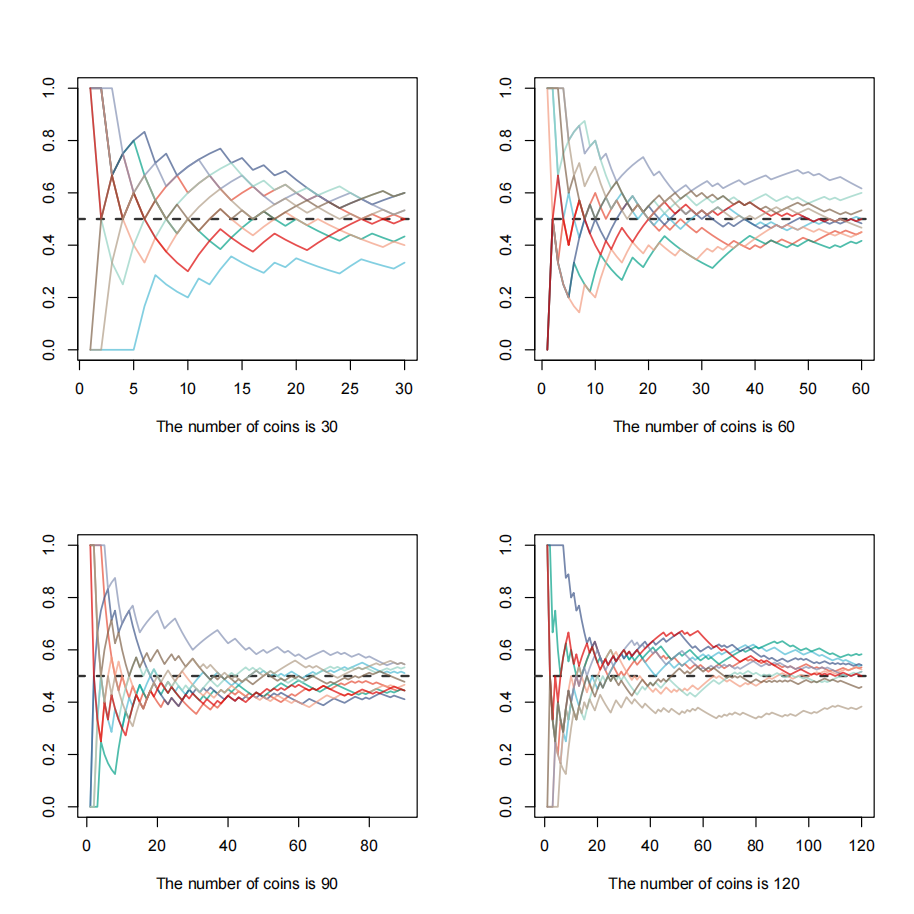
Fig. 12.2 多次抛硬币的结果

请思考一下以下两个问题：

Question

• 从你运行的实验中，你发现了什么相似点？

• 这些相似的结果是否普遍存在的？

Conclusion

• 概率是频率的稳定值；

• 频率 \(X_n\) 与概率 \(p\) 的绝对偏差 \(\left|x_{n}-p\right|\) 将随 \(n\) 增大而呈现主键减小的趋势；

• 由于随机性，绝对偏差 \(\left|x_{n}-p\right|\) 时大时小，虽然无法排除大偏差发生的可能性，但岁 \(n\) 不断增大，大偏差发生的可能性会越来越小。

由此，我们定义随机变量序列的一种收敛性。

收敛性

设 \(\{X_n\}\) 为一随机变量序列，而 \(X\) 为一随机变量。如果对任意的 \(\varepsilon>0\) ，有

\[ \lim _{n \rightarrow \infty} P\left(\left|X_{n}-X\right| \geqslant \varepsilon\right)=0\]

则称序列 \(\{X_n\}\) 依概率收敛于 \(X\) ,记作 \(X_{n} \stackrel{P}{\longrightarrow} X\) 。

Remark

• 在定义中 \(P\left(\left|X_{n}-X\right| \geqslant \varepsilon\right) \rightarrow 0\) ，等价于 \(P\left(\left|X_{n}-X\right|<\varepsilon\right) \rightarrow 1\) ；

• 特别地， \(P(X=c)=1\) 时, 则 \(X_{n}\stackrel{P}{\longrightarrow} c\) 。

Property 12.1 (依概率收敛的四则运算)

设 \(\{X_n\}, \{Y_n\}\) 是两个随机变量序列， \(a,b\) 是两个常数。如果

\[X_{n} \stackrel{P}{\longrightarrow} a, \quad Y_{n} \stackrel{P}{\longrightarrow} b,\]

则有

• \(X_{n} \pm Y_{n} \stackrel{P}{\rightarrow} a \pm b\) ；

• \(X_{n} \times Y_{n} \stackrel{P}{\rightarrow} a \times b\) ；

• \(X_{n} / Y_{n} \stackrel{P}{\rightarrow} a / b, b \neq 0\) 。

Example 12.2

设随机变量 \(X_n\) 服从柯西分布，其密度函数为

\[p_{n}(x)=\frac{n}{\pi\left(1+n^{2} x^{2}\right)} \quad-\infty<x<\infty.\]

试证 \(X_{n} \stackrel{P}{\rightarrow} 0\) 。

Proof

我们考虑事件 \(\{|X_n - 0|\geq \varepsilon\}\) 发生的概率，即

\[\begin{split} \begin{eqnarray*} P\left(\left|X_{n}-0\right| \geq \varepsilon\right) &=&P\left(\left|X_{n}\right| \geqslant \varepsilon\right) \\ &=&\int_{-\infty}^{-\varepsilon} p_{n}(x) d x+\int_{\varepsilon}^{+\infty} p_{n}(x) d x \\ &=&\int_{-\infty}^{-\varepsilon} \frac{n}{\pi\left(1+n^{2} x^{2}\right)} d x+\int_{\varepsilon}^{+\infty} \frac{n}{\pi\left(1+n^{2} x^{2}\right)} d x \\ &=&\frac{2}{\pi} \int_{\varepsilon}^{+\infty} \frac{1}{\pi\left(1+n^{2} x^{2}\right)} d(n x) \\ &\overset{{n x=\tan u}}{=} & \frac{2}{\pi} \int_{\operatorname{arctan}(n \varepsilon)}^{\frac{\pi}{2}} \frac{1}{1+\tan ^{2} u} \cdot d \operatorname{tan}u\\ &=&\frac{2}{\pi}\left(\left.u\right|_{\arctan (n \varepsilon)} ^{\frac{\pi}{2}}\right) \\ &=&\frac{2}{\pi}\left(\frac{\pi}{2}-\arctan (n \varepsilon)\right) \\ &=& 1-\frac{2}{\pi} \cdot \arctan (n \varepsilon) \rightarrow 0 \end{eqnarray*} \end{split}\]

Question

比较一下，数列的收敛性与随机变量的收敛性。

Question

如果 \(X_{n} \stackrel{P}{\rightarrow} a\) ,那么 \(E\left(X_{n}\right) \rightarrow a\) 成立吗？

接下来我们看下面一个例子。

Example 12.3

考虑一个随机变量，其分布列为

\[\begin{split}P\left(X_{n}=x\right)=\left\{\begin{aligned} &1-\frac{1}{n}, & x=0 \\ &\frac{1}{n}, & x=n^{2} \\ &0, & \text{其他}. \end{aligned}\right.\end{split}\]

Solution

由题可知，

\[P\left(\left|X_{n}\right|>\varepsilon\right)=P\left(X_{n}=n^{2}\right)=\frac{1}{n} \rightarrow 0.\]

因此， \(X_{n} \stackrel{P}{\rightarrow} 0\) 。我们来计算一下 \(X_n\) 的数学期望，即

\[E\left(X_{n}\right)=0 \cdot\left(1-\frac{1}{n}\right)+n^{2} \cdot \frac{1}{n}=n \rightarrow \infty. \]

因此， \(E\left(X_{n}\right) \rightarrow 0\) 。