8.1. 引导问题：一维 vs 多维

当我们想要研究本学期某一个学生的概率论与数理统计的期末成绩，记其为 \(X_1\) 。显然， \(X_1\) 是一个随机变量，其取值应该是从 0 至 100 之间的自然数。此时，我们并不知道期末考试成绩的分布，所以，我们也无法预测某一位同学的期末成绩。

值得注意的是，在课程大纲中，高等数学和线性代数列为概率论与数理统计的先修课程。记其高等数学的期末成绩为 \(X_2\) ，而线性代数的期末成绩为 \(X_3\) 。图 Fig. 8.1 是高等数学、线性代数分别与概率论与数理统计期末考试的散点图。

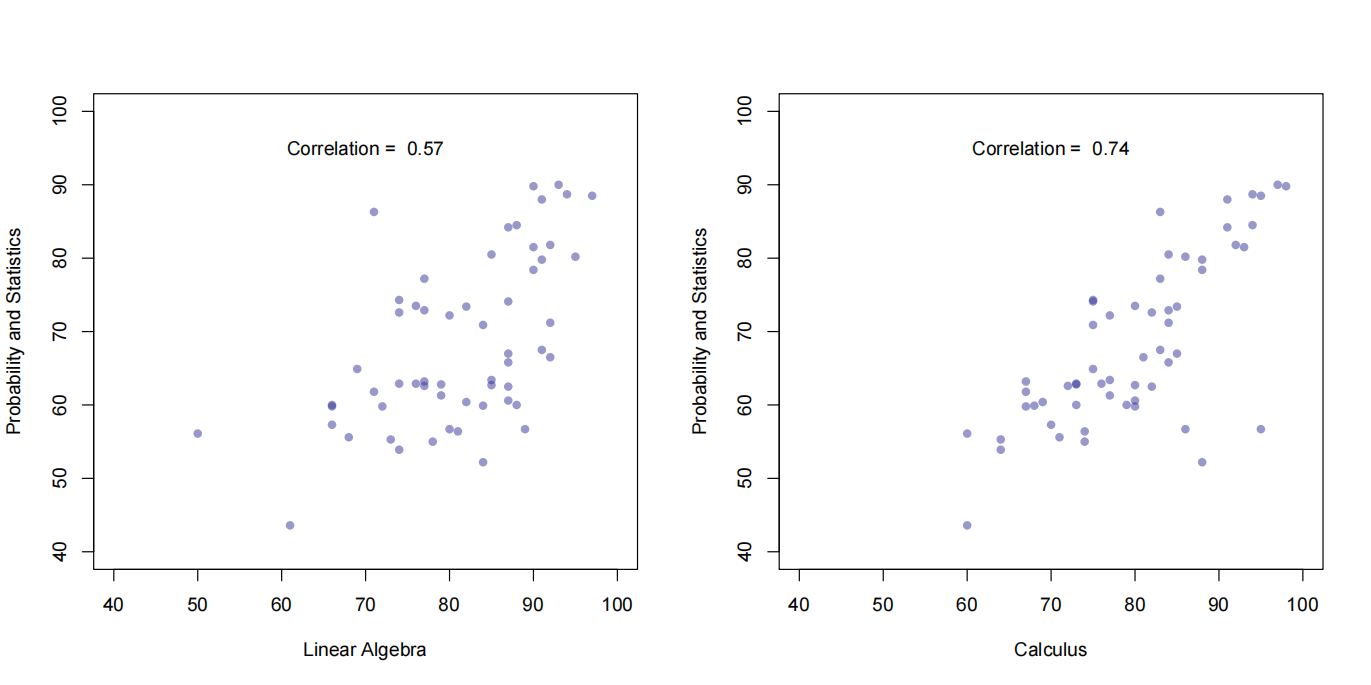
Fig. 8.1 两门先修课程与《概率论与数理统计》课程期末成绩的关系

如果我们研究清楚 \(X_1,X_2,X_3\) 之间的关系，那么我们可以通过已知的 \(X_2\) 和 \(X_3\) 来预测未知的 \(X_1\) 。这就是一般建模的逻辑。因此，如何同时研究多个随机变量是必要的。